If you’ve delved into the realm of machine learning, it’s very likely that you’ve heard of neural networks. They were once a novel idea to approach the problem of programming computers to make decisions on their own – the early days of artificial intelligence. Over the years they fell out of use due to their large computational cost and it was only in recent years that our technology has caught up to these methods in terms of storage and processing power. Now a Neural Network (NN) is one of the fundamental machine learning algorithms data scientists must be familiar with.
I feel that the original description of NN nodes to be a bit mystifying. Stemming from the neural networks within our brains, neural networks can be thought of as nodes that are activated. However, the thought of teaching a computer to ‘activate’ a node always stumped me. Instead, thinking of neural networks as a series of nodes that are weighted has been much easier for me, personally, to digest.
Let’s take two terms, x1 and x2, that are binary – they can either be 0 or 1 – and we want to create an algorithm that can make a decision based on how these two terms relate to each other.
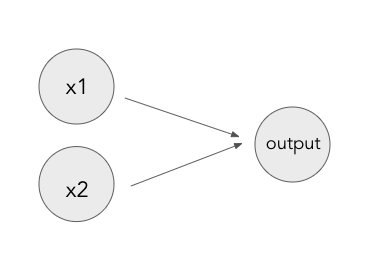
The decision can be made by passing these terms to nodes that will output a “decision” based on the value passed to them. This decision is determined by a function, called the activation function. A common activation function for logistic regression and classification problems is the sigmoid function, which returns values close to 0 for negative inputs and vales close to 1 for positive inputs.
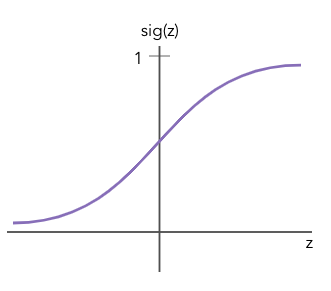
The input to a node is the linear combination (or weighted sum) of the terms and the node will output a result from the sigmoid function. So the goal is to weight the inputs to that function so that they reproduce the decision you’re aiming for.
Let’s consider a very simple NN for the binary AND function – it should return 1 if x1 and x2 are both 1 and 0 otherwise. We want to weight x1 and x2 so that when they are both 1, the sigmoid function is positive and returns 1. However, if both of the terms are 0, the sum of the terms will also be zero. For the sigmoid to return 0, we need the input to be negative. This can be handled by adding an additional term, with a value equal to 1, known as the bias.
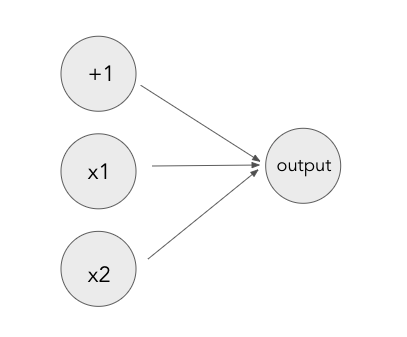
Now let’s consider all four options for this binary function. For each result we can determine if input of the sigmoid function needs to be positive or negative
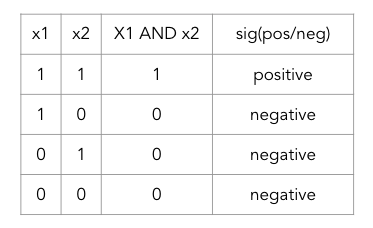
From there we can choose weights for each of the terms, x1, x2 and the bias, to produce the correct sign on the input
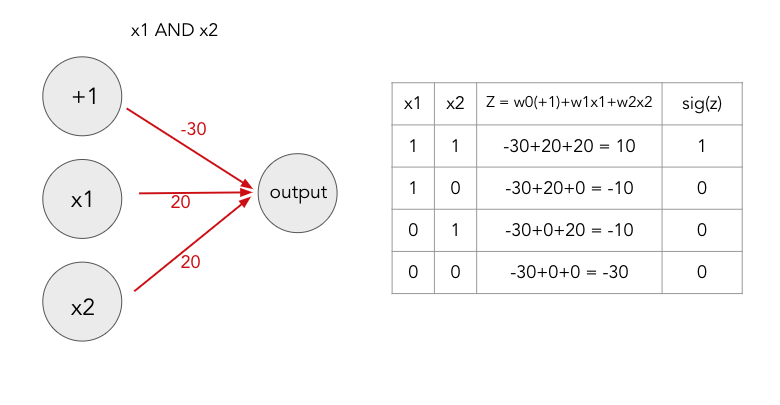
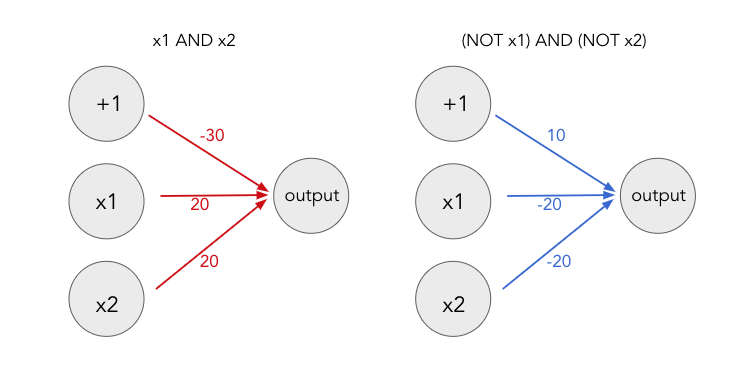
Our NN now reproduces the AND function! What if we wanted to reproduce a more complicated binary function, like XNOR – it returns 1 if x1 and x2 are the same, either 1 or 0, and returns 0 if they are different. The first part of the decision, returning 1 if x1 and x2 are the same, are two different AND functions. One for x1 AND x2 and one for (NOT x1) AND (NOT x2).
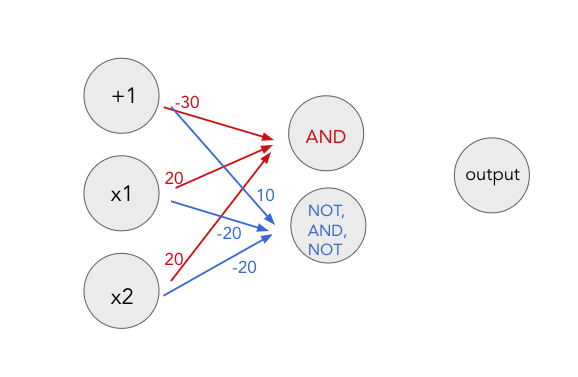
To consider these two decisions at once, we can construct a NN that has multiple layers. The middle layer, called the hidden layer, handles the results of the first two decisions. These nodes use the results of the two AND functions to make the final decision.
However, these nodes need to be connected with another type of decision to achieve the final XNOR result. We need to accept results from node 1 (x1 AND x2) OR node 2 ((NOT x1) AND (NOT x2)). This final layer connects the nodes from the first decisions.
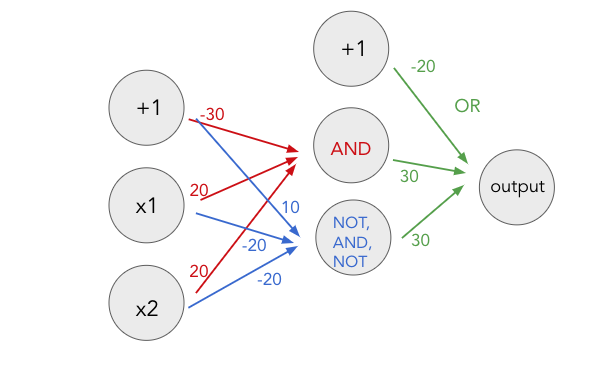
Here we can see how the weights of nodes can be fit to allow the network to make specific decisions. This simplistic binary model makes it easier to conceptualize how a NN is tuned to a specific decision. These decisions can then be layered to make more complex decisions. When constructing a NN, the decisions made by nodes are not concretely defined by the data scientist and instead are molded by the training set. By training the NN, the model adjusts the weights to each node to reproduce the decisions you’ve trained it on – just like how we can determine the weights for the AND function by considering the four possible options. A neural network creates a framework for many weighted decisions. This kind of model makes it possible for computer algorithms to tackle large-scale classification problems.
sources:
- Andrew Ng’s Machine Learning Coursera Course
- MIT News, Explained: Neural Networks https://news.mit.edu/2017/explained-neural-networks-deep-learning-0414

No responses yet